6.1 Areas Between Curves/10

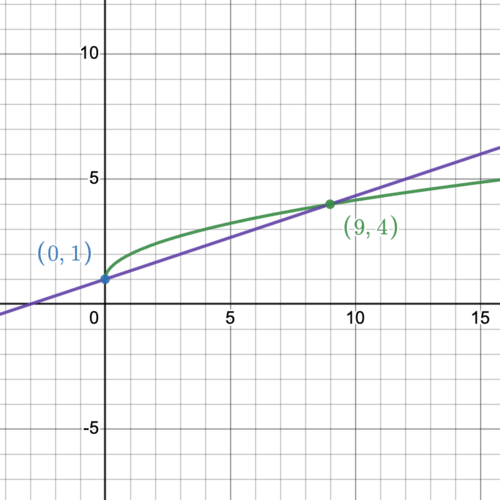
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align} & \color{red}\mathbf{y=1+\sqrt{x}} & \color{royalblue}\mathbf{y=\frac{3+x}{3}} \\ \\ \end{align} }

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align} &1+\sqrt{x} = \frac{3+x}{3} \\[2ex] &= 1+\sqrt{x}-\frac{3+x}{3} = 0 \\ &= \frac{3+3\sqrt{x}}{3}-\frac{3+x}{3} = 0 \\ &= 3+3\sqrt{x}-3+x = 0 \\ &= 3\sqrt{x}+x = 0 \\ &= 3\sqrt{x} = -x \\ &= 9x = x^2 \\ &= 9x-x^2 = 0 \\ &= x(9-x) = 0 \\ &= x = 0,9 \end{align} }