7.1 Integration By Parts/54: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (17 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
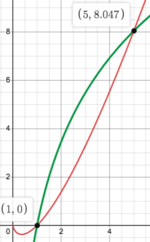
[[File:54.png|right|150px|]] | |||
<math> | <math> | ||
y=5\ln(x) , y=x\ln(x) | y={ \color{OliveGreen}5\ln(x) }, y={ \color{Red}x\ln(x)} | ||
</math> | </math> | ||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
| Line 12: | Line 13: | ||
&x=1 \\[1ex] | &x=1 \\[1ex] | ||
\end{align} | |||
</math> | |||
When <math> x=2 </math>, | |||
<math> | |||
5\ln(2) > 2\ln(2) | 5\ln(2) > 2\ln(2) | ||
</math> | </math> | ||
<math> | <math> | ||
\int_{1}^{5}\left(5\ln(x) -x\ln(x) \right)dx = \int_{1}^{5} \left(5\ln(x) \right)dx - \int_{1}^{5} \left(x\ln(x) \right)dx | \int_{1}^{5}\left(5\ln(x) -x\ln(x) \right)dx = {\color{NavyBlue}\int_{1}^{5} \left(5\ln(x) \right)dx} - {\color{RedOrange}\int_{1}^{5} \left(x\ln(x) \right)dx } =25\ln(5)-20 - \left(\frac{25}{2}\ln(5) - 6 \right) = \frac{25}{2} \ln(5) -14 | ||
</math> | </math> | ||
| Line 25: | Line 29: | ||
<math> | <math> | ||
\begin{align} | \begin{align} | ||
\int_{1}^{5} \left(5\ln(x) \right)dx = 5 \int_{1}^{5} \left(\ln(x) \right)dx = 5\left(x\ln(x)\bigg|_{1}^{5}- \int_{1}^{5} \left(\frac{x}{x} \right)dx \right) = 5\left(x\ln(x) \bigg|_{1}^{5}- x \bigg|_{1}^{5} \right) = 5\left(5\ln(5)-1\ln(1) - \left(5-1 \right) \right) = 25\ln(5)-20 \\ | {\color{NavyBlue}\int_{1}^{5} \left(5\ln(x) \right)dx } &= 5 \int_{1}^{5} \left(\ln(x) \right)dx = 5\left(x\ln(x)\bigg|_{1}^{5}- \int_{1}^{5} \left(\frac{x}{x} \right)dx \right) = 5\left(x\ln(x) \bigg|_{1}^{5}- x \bigg|_{1}^{5} \right) = 5\left(5\ln(5)-1\ln(1) - \left(5-1 \right) \right) = 25\ln(5)-20 \\[2ex] | ||
u &= \ln(x) \quad dv= 1 dx \\ | u &= \ln(x) \quad dv= 1 dx \\ [2ex] | ||
du &= \frac{1}{x} dx \quad v=x \\ | du &= \frac{1}{x} dx \quad v=x \\ [2ex] | ||
\end{align} | \end{align} | ||
| Line 34: | Line 38: | ||
<math> | <math> | ||
\int_{1}^{5} \left(x\ln(x) \right)dx = \frac{x^2\ln(x)}{2}\bigg|_{1}^{5} - \int_{1}^{5} \left(\frac{x^2}{2x} \right)dx = \frac{x^2\ln(x)}{2}\bigg|_{1}^{5} - \frac{1}{2}\int_{1}^{5} \left(x \right)dx = \frac{1\ln(1)}{2}-\frac{25\ln(5)}{2} -\left(\frac{1}{2}\right) \left( \frac{x^2}{2} \right) \bigg|_{1}^{5} = 0-\frac{25}{2}\ln(5) - | {\color{RedOrange}\int_{1}^{5} \left(x\ln(x) \right)dx }= \frac{x^2\ln(x)}{2}\bigg|_{1}^{5} - \int_{1}^{5} \left(\frac{x^2}{2x} \right)dx = \frac{x^2\ln(x)}{2}\bigg|_{1}^{5} - \frac{1}{2}\int_{1}^{5} \left(x \right)dx = \frac{1\ln(1)}{2}-\frac{25\ln(5)}{2} -\left(\frac{1}{2}\right) \left( \frac{x^2}{2} \right) \bigg|_{1}^{5} = 0-\frac{25}{2}\ln(5) -\left(\frac{25-1}{4}\right) = \frac{25}{2}\ln(5) - 6 | ||
</math> | </math> | ||

![{\displaystyle {\begin{aligned}5\ln(x)&=x\ln(x)\\[1ex]&x=5\\[1ex]&x=1\\[1ex]\end{aligned}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7ecb8b4109c7b052ff090a770a426d465b1ce8f1)



![{\displaystyle {\begin{aligned}{\color {NavyBlue}\int _{1}^{5}\left(5\ln(x)\right)dx}&=5\int _{1}^{5}\left(\ln(x)\right)dx=5\left(x\ln(x){\bigg |}_{1}^{5}-\int _{1}^{5}\left({\frac {x}{x}}\right)dx\right)=5\left(x\ln(x){\bigg |}_{1}^{5}-x{\bigg |}_{1}^{5}\right)=5\left(5\ln(5)-1\ln(1)-\left(5-1\right)\right)=25\ln(5)-20\\[2ex]u&=\ln(x)\quad dv=1dx\\[2ex]du&={\frac {1}{x}}dx\quad v=x\\[2ex]\end{aligned}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/25d25c0f3562f14a2719a35ea2cea6a5b8a0b4b0)

