6.1 Areas Between Curves/13: Difference between revisions
No edit summary |
No edit summary |
||
| Line 3: | Line 3: | ||
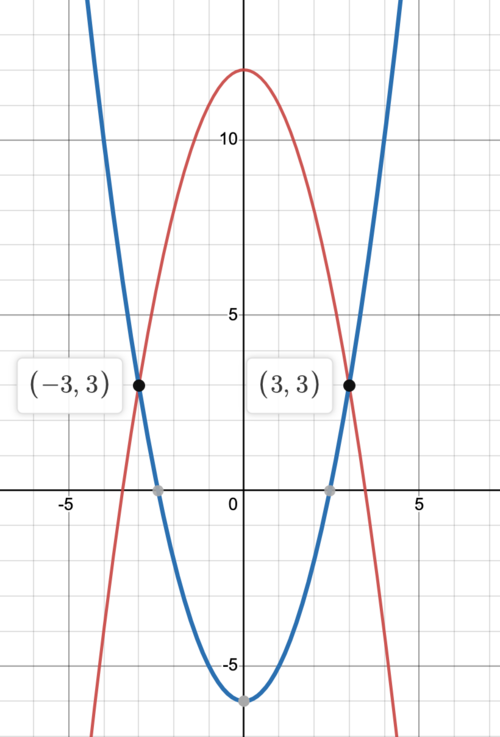
<math>\color{blue}{y=x^2-6}</math> | <math>\color{blue}{y=x^2-6}</math> | ||
[[File:Screen Shot 2022-09-20 at 1.07.09 PM.png|right|500px]] | |||
<math>\int_{-3}^{3} \left|(12-x^2) - (x^2-6) \right| dx </math> | <math>\int_{-3}^{3} \left|(12-x^2) - (x^2-6) \right| dx </math> | ||
Latest revision as of 20:12, 20 September 2022
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \color{red}{y=12-x^2}}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \color{blue}{y=x^2-6}}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \int_{-3}^{3} \left|(12-x^2) - (x^2-6) \right| dx }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align} 12-x^2 &= x^2-6 \\ 18 &= 2x^2 \\ 9 &=x^2 \\ \pm3 &= x \end{align} }
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align} \int_{-3}^{3} \left|(12-x^2) - (x^2-6) \right| dx &= [(12x-\frac{1}{3}x^3) - (\frac{1}{3}x^3 - 6x)] \Bigg|_{-3}^{3} \\ & = [(12(3) - \frac{1}{3}(3)^3) - (\frac{1}{3}(3)^3-6(3) )] - [(12(-3) - \frac{1}{3}(-3)^3) - (\frac{1}{3}(-3)^3-6(-3) )] \\ & = 36-(-36) \\ & = 72 \end{align} }