6.1 Areas Between Curves/22

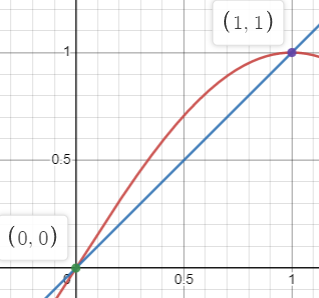Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align} & \color{red}\mathbf{y= \sin(\frac{\pi x}{2})} & \color{royalblue}\mathbf{y=x} \\ \end{align} }

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align} \sin(\frac{x\pi}{2}) &= x \\ x &= 0 \\ x &=1 \\ \end{align} }

Failed to parse (Conversion error. Server ("https://en.wikipedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \int _{0}^{1}\left(\sin \left({\frac {x\pi }{2}}\right)-x\right)dx}

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \begin{align} \int_{0}^{1} \left(\sin(\frac{x\pi}{2})\right)dx &= \int_{0}^{\frac{\pi}{2}} \sin(u)du \\ & u = \frac{x\pi}{2} \\ & du = \frac{\pi}{2}dx \\ & \frac{2}{\pi}du=dx \\ \end{align} }

New upper limit: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{(0)\pi}{2}=0 }

New lower limit: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{(1)\pi}{2} = \frac{\pi}{2} }